Maximum cut

For a graph, a maximum cut is a cut whose size is at least the size of any other cut. The problem of finding a maximum cut in a graph is known as the max-cut problem.

The problem can be stated simply as follows. One wants a subset S of the vertex set such that the number of edges between S and the complementary subset is as large as possible.

There is a more advanced version of the problem called weighted max-cut. In this version each edge has a real number, its weight, and the objective is to maximize not the number of edges but the total weight of the edges between S and its complement. The weighted max-cut problem is often, but not always, restricted to non-negative weights, because negative weights can change the nature of the problem.

Contents

Computational complexity

The following decision problem related to maximum cuts has been studied widely in theoretical computer science:

Given a graph G and an integer k, determine whether there is a cut of size at least k in G.

This problem is known to be NP-complete. It is easy to see that problem is in NP: a yes answer is easy to prove by presenting a large enough cut. The NP-completeness of the problem can be shown, for example, by a transformation from maximum 2-satisfiability (a restriction of the maximum satisfiability problem).[1] The weighted version of the decision problem was one of Karp's 21 NP-complete problems;[2] Karp showed the NP-completeness by a reduction from the partition problem.

The canonical optimization variant of the above decision problem is usually known as the maximum cut problem or max-cut problem and is defined as:

Given a graph G, find a maximum cut.

Polynomial-time algorithms

As the max-cut problem is NP-hard, no polynomial-time algorithms for max-cut in general graphs are known. However, a polynomial-time algorithm to find maximum cuts in planar graphs exists.[3]

Approximation algorithms

There is a simple randomized 0.5-approximation algorithm: for each vertex flip a coin to decide to which half of the partition to assign it.[4][5] In expectation, half of the edges are cut edges. This algorithm can be derandomized with the method of conditional probabilities; therefore there is a simple deterministic polynomial-time 0.5-approximation algorithm as well.[6][7] One such algorithm is: given a graph 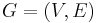G = (V, E) start with an arbitrary partition of V and move a vertex from one side to the other if it improves the solution until no such vertex exists. The number of iterations is bound by 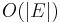O ( \left | E \right | ) because the algorithm improves the cut value by at least 1 at each step and the maximum cut is at most 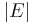\left | E \right |. When the algorithm terminates, each vertex 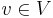v \in V has at least half its edges in the cut (otherwise moving v to the other subset improves the solution). 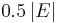Therefore the cut is at least 0.5 \left | E \right |.

The best known max-cut algorithm is the 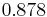0.878…-approximation algorithm by Goemans and Williamson using semidefinite programming and randomized rounding.[8][9] It has been shown by Khot et al that this is the best possible approximation ratio for Max-Cut assuming the unique games conjecture.

Inapproximability

The max-cut problem is APX-hard,[10] meaning that there is no polynomial-time approximation scheme (PTAS), arbitrarily close to the optimal solution, for it, unless P = NP. Moreover, it has been shown NP-hard to approximate the max-cut value to better than 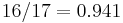16/17=0.941….[11][12]

Assuming the unique games conjecture (UGC), it is in fact NP-hard to approximate the max-cut value by a factor of 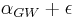\alpha_{GW} %2B \epsilon for any 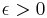\epsilon > 0, where 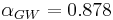\alpha_{GW} = 0.878… is the approximation factor of Goemans–Williamson.[13] In other words, assuming the UGC and that 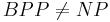BPP \neq NP, the Goemans–Williamson algorithm yields essentially the best polynomial-time-computable possible approximation ratio for the problem.

Maximum bipartite subgraph

A cut is a bipartite graph. The max-cut problem is essentially the same as the problem of finding a bipartite subgraph with the most edges.

Let 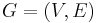G=(V,E) be a graph and let 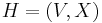H=(V,X) be a bipartite subgraph of G. Then there is a partition (S, T) of V such that each edge in X has one endpoint in S and another endpoint in T. Put otherwise, there is a cut in H such that the set of cut edges contains X. Therefore there is a cut in G such that the set of cut edges is a superset of X.

Conversely, let 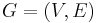G=(V,E) be a graph and let X be a set of cut edges. Then 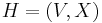H=(V,X) is a bipartite subgraph of H.

In summary, if there is a bipartite subgraph with k edges, there is a cut with at least k cut edges, and if there is a cut with k cut edges, there is a bipartite subgraph with k edges. Therefore the problem of finding a maximum bipartite subgraph is essentially the same as the problem of finding a maximum cut.[14] The same results on NP-hardness, inapproximability and approximability apply to both the maximum cut problem and the maximum bipartite subgraph problem.

See also

Notes

  1. ^ Garey & Johnson (1979).
  2. ^ Karp (1972).
  3. ^ Hadlock (1975).
  4. ^ Mitzenmacher & Upfal (2005), Sect. 6.2.
  5. ^ Motwani & Raghavan (1995), Sect. 5.1.
  6. ^ Mitzenmacher & Upfal (2005), Sect. 6.3.
  7. ^ Khuller, Raghavachari & Young (2007).
  8. ^ Gaur & Krishnamurti (2007).
  9. ^ Ausiello et al. (2003)
  10. ^ Papadimitriou & Yannakakis (1991) prove MaxSNP-completeness.
  11. ^ Håstad (2001)
  12. ^ Trevisan et al. (2000)
  13. ^ Khot et al. (2007).
  14. ^ Newman (2008).

References

Maximum cut (optimisation version) is the problem ND14 in Appendix B (page 399).
Maximum cut (decision version) is the problem ND16 in Appendix A2.2.
Maximum bipartite subgraph (decision version) is the problem GT25 in Appendix A1.2.

Further reading

External links